| Collective Behavior of Self-propelled Particles |
|---|
|
| Simulation of Nucleation and "Critical Clusters" |
|---|
|
| Simulation of Colloidal Systems under Confinement and Shear | |
|---|---|
 | In the framework of the transregional collaborative research center TR6 "Physics of colloidal dispersions in external fields" we study colloid-polymer mixtures confined in either slit pores or cylindrical pores, focusing on the interplay between finite size and surface effects on the possible phase separation between polymer-rich and colloid-rich phases, and on the structure of such systems under steady-state shear. In a variety of closely related subprojects, also the effects of confinement on one- or two-component colloidal crystals are studied, and the mechanical distortion of their struture caused by lateral compression, and the response of a dense colloidal dispersion is studied when one colloidal particle is dropped through the system ("microrheology"). Finally, also phase separation in mixtures of rodlike and spherical colloids is studied. For this research, we collaborate with J. Horbach (DLR Cologne), H. Löwen and S. Egelhaaf (University of Düsseldorf), P. Nielaba and G. Maret (University of Konstanz) and T. Schilling (University of Luxembourg). For more information, contact Kurt Binder and/or Peter Virnau. |
| Ising Models with Random Fields, with Gradients, Surface Fields, or Shear | |
|---|---|
 | While the Ising model is a kind of "fruitfly" of statistical mechanics, and its basic aspects are hence covered in all corresponding textbooks, for the development of Monte Carlo methods to study phase transitions the Ising model continues to be the major "workhorse", and thus continues to play an important role in the Condensed Matter Theory Group. In fact, this role is evident from two of the most well-known textbooks on Monte Carlo methods that have emerged from this group (D.P. Landau and K. Binder, A Guide to Monte Carlo Methods in Statistical Physics, 3rd ed.; Cambridge Univ. Univ. Press, Cambridge, 2009; K. Binder and D.W. Heermann, Monte Carlo Simulation in Statistical Physics. An Introduction. 5th ed.; Springer, Berlin, 2010), and from specific studies: e.g., the finite size scaling of the Ising model in random fields has been clarified; the phase transition of Ising films where surface fields compute with a field gradient in the bulk has been elucidated; the order parameter distribution of Ising strips or elongated tubes has been studied, to demonstrate the transition from single- domain to multiple-domain structure; finally, the anisotropic critical behavior of Ising systems under shear has been studied. Also methods to estimate wall free energies, contact angles of wall-attached droplets, line tensions, etc., have been first tested with the Ising model, before any attempt to use such methods for more complicated off-lattice models has been made. These studies have been part of a widespread collaborative effort, involving D. P. Landau (Center of Simulational Physics at the University of Georgia), E.V. Albano (University of La Plata/Argentina), and R.C.L. Vink (the University of Göttingen). For more information, please contact Kurt Binder and/or Peter Virnau. |
| The Interface between Graphite and Polybutadiene Melts: A Model System for a Polymer-Solid Contact |
|
|---|---|
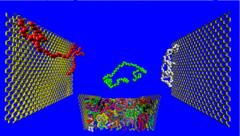 | In the framework of the priority program SPP 1369 "polymer-solid contacts" of the German Research Foundation (DFG) we simulate an atomistically realistic model for fluid polybutadiene confinded in a slit pore between two graphite walls, and study over which scale the walls modity structure and dynamics of the polymers, and characterize the resulting nanoscale "interphase" layers. These simulations require huge computer ressources and are done in collaboration with W. Paul of the University of Halle using the massively parallel JUGENE supercomputer at Jülich. For more information, please contact Kurt Binder and/or Peter Virnau. |
| Knots in Polymers, Proteins and DNA |
|---|
|
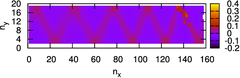
 Dynamical collective behavior observed in, e.g., schools of fish and flocks of birds can often be described with simple models of so-called self-propelled particles. Even complex behavior can be reproduced by simple rules that are followed by all individuals (e.g., follow your neighbors but do not bump into them). On the microscale, both bacteria and colloidal particles have emerged as model systems to study a wealth of different phenomena such as swirling, swarming, and turbulence.
Dynamical collective behavior observed in, e.g., schools of fish and flocks of birds can often be described with simple models of so-called self-propelled particles. Even complex behavior can be reproduced by simple rules that are followed by all individuals (e.g., follow your neighbors but do not bump into them). On the microscale, both bacteria and colloidal particles have emerged as model systems to study a wealth of different phenomena such as swirling, swarming, and turbulence. 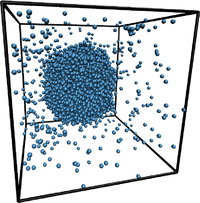 Metastable phases decay by rare statistical fluctuations, termed "nucleation", where a "critical cluster" (i.e., a nanoscopic aggregate of the new phase having the minimal size to be able to grow) forms. Such critical clusters may form in the bulk ("homogeneous nucleation"), which facilitate this cluster formation by reducing the free energy barrier that needs to be overcome. Specialized computer simulation methods are developed to estimate the surface excess free energies, that control these processes, and related quantities (such as contact angles, line tension, Tolman length). This research is carried out in the framework of the priority program SPP 1296 "Heterogeneous Nucleation and Structure Formation" of the German Research Foundation (DFG), and we collaborate with J. Horbach (DLR Cologne) and S. Egelhaaf and H. Löwen (University of Düsseldorf), where complementary studies are done, as well as with S. K. Das (Bangalore) and S. Puri (New Delhi, India). For more information, please contact
Metastable phases decay by rare statistical fluctuations, termed "nucleation", where a "critical cluster" (i.e., a nanoscopic aggregate of the new phase having the minimal size to be able to grow) forms. Such critical clusters may form in the bulk ("homogeneous nucleation"), which facilitate this cluster formation by reducing the free energy barrier that needs to be overcome. Specialized computer simulation methods are developed to estimate the surface excess free energies, that control these processes, and related quantities (such as contact angles, line tension, Tolman length). This research is carried out in the framework of the priority program SPP 1296 "Heterogeneous Nucleation and Structure Formation" of the German Research Foundation (DFG), and we collaborate with J. Horbach (DLR Cologne) and S. Egelhaaf and H. Löwen (University of Düsseldorf), where complementary studies are done, as well as with S. K. Das (Bangalore) and S. Puri (New Delhi, India). For more information, please contact 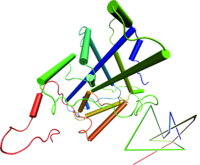 Although globular homopolymers are typically highly knotted, less than one in a hundred protein structures contain a knot ( http://knots.mit.edu ). Nevertheless, intriguing counter-examples exist, like the most complicated protein knot, which was discovered recently during a diploma thesis in our group (see figure on the left). Apart from analyzing biological data, we perform Monte Carlo simulations of simplified protein and DNA models to learn more about entanglements in viral DNA, chromatin and proteins. On this topic, we collaborate with theory groups at MIT and an experimental group at the MPI for Polymer Research. If you are interested in interdisciplinary investigations at the frontier of physics, mathematics and molecular biology, please contact
Although globular homopolymers are typically highly knotted, less than one in a hundred protein structures contain a knot ( http://knots.mit.edu ). Nevertheless, intriguing counter-examples exist, like the most complicated protein knot, which was discovered recently during a diploma thesis in our group (see figure on the left). Apart from analyzing biological data, we perform Monte Carlo simulations of simplified protein and DNA models to learn more about entanglements in viral DNA, chromatin and proteins. On this topic, we collaborate with theory groups at MIT and an experimental group at the MPI for Polymer Research. If you are interested in interdisciplinary investigations at the frontier of physics, mathematics and molecular biology, please contact